Add to Favourites
To login click here
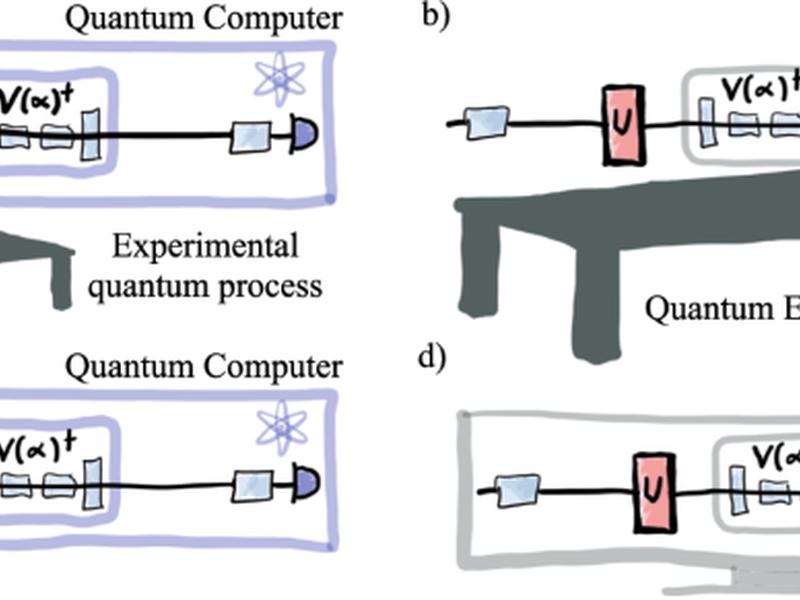
In this work, we consider the task of Quantum Machine Learning (QML) to learn an unknown n-qubit unitary. We employ the framework of statistical learning theory to quantify the prediction performance of the trained QNN. We numerically illustrate our analytical results by showing that the short time evolution of a Heisenberg spin chain can be well learned using only product state training data. We further perform noisy simulations to demonstrate how the noise accumulated preparing highly entangled states can prohibit training. Our results suggest a new quantum-inspired classical approach to unitary compilation, implying that a low-entangling unitary can be compiled using only low-entangled training states.
