Learning Continuous Models For Continuous Physics

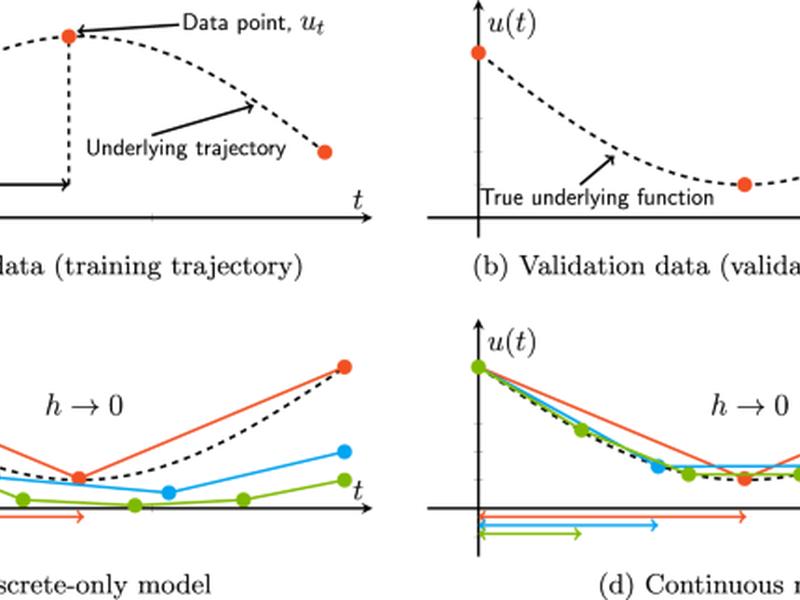
Dynamical systems are important for many scientific and engineering applications, and can often be described by differential equations which evolve continuously in time. Machine learning techniques have recently been shown to provide a powerful approach to model and learn from discrete data, and many scientific fields make extensive use of data-driven methods for describing, discovering, identifying, predicting, and controlling dynamics. These approaches include purely data-driven methods that learn from observational data points, adding constraints to ML methods that aim to respect the relevant physics, and/or hybrid methods combining classical numerical solvers with deep learning.