Sparse Identification Of Lagrangian For Nonlinear Dynamical Systems Via Proximal Gradient Method

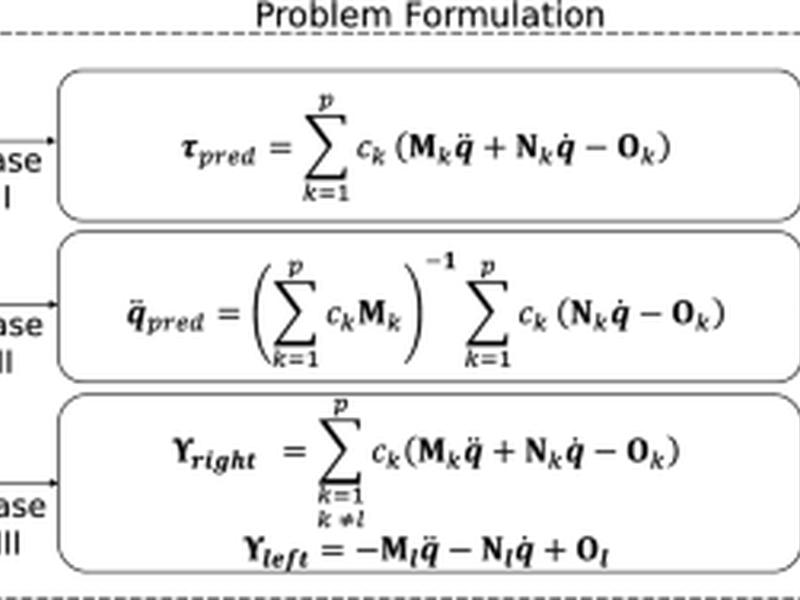
This article discusses the development of a noise-tolerant computational method for extracting the governing equations of nonlinear mechanical systems from data with noise. The method, called xL-SINDy, is an extended version of Lagrangian-SINDy and incorporates the concept of SINDy and the proximal gradient method to obtain sparse Lagrangian expressions. The effectiveness of xL-SINDy was demonstrated using four mechanical systems and compared with SINDy-PI, a robust variant of SINDy. The results show that xL-SINDy is much more robust than existing methods for extracting governing equations from data with noise.